Department of physics
Sie sind hier: UHH >Physics Department > About the Department > Institute und Forschungseinrichtungen > 1. Institut f. theor. Physik > Group Pfannkuche > Team > Prada
Research Projects
Pseudo-spin dynamics in Dirac Hamiltonians
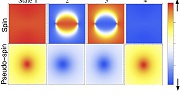
We investigate the spin (upper row of figure) and pseudo-spin (lower row) degrees of freedom in the proximity of a Dirac point (DP). The four-fold degenerate DP splits under the presence of spin-orbit coupling and magnetic field (columns in figure correspond to these four split-off states). As a consequence, intraband transitions are governed by the spin and pseudo-spin texture of the states involved.
Geometric phase in nanomagnets
We investigate non-trivial geometric phases arising in nanomagnets on crystalline surfaces. Those arise as a consequence of the interplay of time reversal and point group symmetries. Owing to their robustness, geometric phases represent a robust resource for storing and processing quantum information.
A generic Hamiltonian with uniaxial and rhombic terms splits the (2m+1) states onto doubly degenerate pairs connected by a time reversal operation. Each degenerate pair is connected by a time-reversal or a rotated-time-reversal operation. Equivalence under both transformations involves a non-trivial geometric phase.
Nano-Electro Mechanical Systems (NEMS)
We study the coupling of the electronic and mechanical degrees of freedom in NEMS. In collaboration with Blick's group and C. Kim's group, we focus on obtaining rectified direct currents in NEMS-based heterostructures. In Applied Phys. Lett. 106, (2015), we investigate the non-linear dynamics from a classical perspective. In Phys. Rev. B 89, 045426 (2014) we investigate the possibility of generating direct currents in coupled nanomechanical resonators by tunable symmetry breaking, and in Phys. Rev. Lett. 111, 197202 (2013), we obtained broadbands of strong nonlinear coupling in nanoelectromechanical electron shuttles. A general theoretical work in double coupled nano pillars is done in Phys. Rev. B 86, 165424 (2013). ACS Nano 6, 651 (2012) is a result of our ongoing collaboration with experimentalists.